Тригонометричните формула - списък на основните формули
Съотношенията между основните функции тригонометричните - задължително, косинус, допирателни, котангенс, и - да тригонометрични формули. И тъй като отношенията между тригонометричните функции много, то това обяснява изобилието на тригонометричните формули. Някои формули свързват тригонометрични функции същия ъгъл, а от друга - множествена функция на ъгъла, а други - да даде възможност да се намали степента, четвъртата - за да изразят всички функции чрез допирателна половин ъгъл и т.н.
В тази статия ще се изброят, за всички основни тригонометрични формули, които са достатъчни, за да се отговори на по-голямата част от проблемите, тригонометрия. За улеснение на съхранение и употреба, се групират според предназначението им, както и да ги сложи в таблицата.
Навигация в страниците.
Основни тригонометрични идентичности
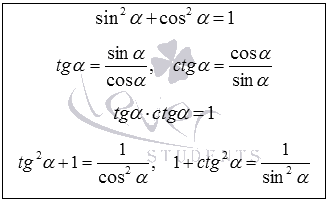
Основни тригонометрични идентичности, определени отношения между синус, косинус, тангенс и котангенс на ъгъла. Те са получени от определението на синус, косинус, допирателна и котангенс и концепции на единица кръг. Те позволяват да експресират един тригонометрична функция чрез всяка друга.
Подробно описание на тригонометрични формули и техните деривация и приложни примери вижте статията основни тригонометрични идентичност.
формули намаляване


Намаляване формули следват от свойствата на синус, косинус, тангенс и котангенс. тоест, те отразяват собственост на периодичността на тригонометричните функции, симетрията на имота, както и офсетов имота под определен ъгъл. Тези тригонометрични формули позволяват да се работи с произволни ъгли се движат, за да работят с ъгли в диапазона от нула до 90 градуса.
Обосновка на тези формули мнемонични за тяхното съхранение и примери за тяхното прилагане може да бъде изследван в статията донесе формула.
добавяне на формули

Тригонометрични добавяне формули показват как тригонометрични функции сума или разлика на два ъгъла, изразени по отношение на тригонометрични функции на ъгли. Тези уравнения служат като основа за получаване на следните тригонометрични формули по-долу.
За повече информация в статията добавяне формули.
Формула на двойни, тройни и т.н. ъгъл


Формула на двойни, тройни и т.н. ъгъл (наричани още няколко ъглови формули) показват как тригонометрични функции на двоичен третични и т.н. ъгъл () са изразени по отношение на тригонометрични функции единствен ъгъл. Тяхното заключение се основава на добавяне формулите за.
Половината ъгъл формула

Половин ъгъл формула показват как тригонометричните функции се изразяват чрез половин ъгъл на косинус на ъгъла. Тези тригонометрични формули следват от двойно ъгъл.
Техните деривация и прилагане примери могат да бъдат намерени в статията на Формула половин ъгъл.
Намаляването на формула


Тригонометрични формули, предназначени за намаляване на степента, до улесняване на прехода от естествените сили на тригонометрични функции към Синеш и уюта в първа степен, но няколко ъгъла. С други думи, те позволяват по-ниска степен на първите тригонометричните функции.
Формула сума и разлика на тригонометрични функции

Основната цел на сумата и разликата формули на тригонометрични функции на е да се премине към характеристиките на продукта, които са много полезни за опростяване на тригонометрични изрази. Тези формули са широко използвани за решаване на тригонометрични уравнения, тъй като те позволяват да се факторизиране сума и разлика от Sines и уюта.
Получаване на формули и техни примери за приложение, виж статията на Формула сума и разлика синус и косинус.
формула продукт на синус, косинус и задължително и косинус

Преходът от продукта от тригонометричните функции на сумата или разликата извършва от Формули работи синус, косинус и задължително косинус.
Universal смяна тригонометрични

Преглед на основните тригонометрия формули завършва с претенциите, които експресират тригонометрични функции по отношение на допирателната на половин ъгъл. Тази замяна се нарича заместване универсален тригонометрични. Нейната удобство е, че всички тригонометрични функции, изразени по тангенс на ъгъла на половината рационално без корени.