Разтворът от уравнения в числа - математика
Моята курсова работа е посветена на един от най-интересните части от теорията на числата - решаването на уравнения в цели числа.
Решение в цели числа на алгебрични уравнения с цели коефициенти с повече от един непознат е един от най-трудните проблеми в теорията на числата.
Проблемът за решаване на уравнения в числа напълно разрешени само за уравнения от втора степен в две неизвестни. Имайте предвид, че за уравнения на всяка степен с едно неизвестно то не представлява значителен интерес, тъй като този проблем може да бъде решен с помощта на определен брой проби. За горните уравнения от втора степен с две и повече неизвестни че е много трудно, не само на проблема с намирането на всички решения в цели числа, но дори една проста задача на установяване на наличието на краен или безкраен набор от такива решения.
В моя проект аз се опитах да се очертаят някои от основните резултати, получени в областта на теорията; решаване на уравнения в числа. Теорема формулирани в него, са снабдени с доказателства в случаите, когато доказателствата доста просто.
1. уравнение с едно неизвестно
Помислете първо уравнение степен с едно неизвестно
Нека коефициентите на уравнението и - числа. Ясно е, че решението на този уравнение
Това е цяло число, само ако е неделими от. По този начин уравнение (1) не винаги е разтворим в числа; например, от две уравнения и първото решение има цяло число и второ число в неразтворим.
Със същото обстоятелство се срещаме в случай на уравнения от степен по-висока от първата: квадратното уравнение има целочислени решения; уравнение в числа е неразрешим, тъй като корените са ирационално.
Проблемът за намиране на корените на уравнението по-голямо от п-та степен с цели коефициенти
Той е решен лесно. Всъщност, дори и - корен на това уравнение. след това
От последното уравнение показва, че дели; Следователно, всеки корен на уравнение (2) е делител константа уравнение. За да намерите число решения на уравнението е необходимо да се изберат тези подгрупи, че когато заместен в уравнението става за самоличност. Например, числата 1, 1, 2, -2, представляващи всички делителите константа уравнение
Само -1 е корен. Ето защо, това уравнение има един корен. Същият метод е лесно да се докаже, че уравнението
в числа е нерешим.
От много по-голям интерес е решението в цели числа на уравнението с много неизвестни.
Прочетете повече: уравнението от първа степен с две неизвестни
Информация за "решаване на уравнения в цели числа"
Категория: Математика
Брой знаци с интервалите: 24303
Брой на маси: 27
Брой на изображения: 7
под формата на рецепти, няма индикация за това как те са открити. Въпреки високото ниво на развитие на алгебра във Вавилон, в клинообразни текстове • Няма концепция за отрицателно число, както и общи методи за решаване на квадратно уравнение. Както беше решено Diophantus и квадратно уравнение. В "аритметика" Diophantus не систематично изложение на алгебра, но тя съдържа.

фракционни преобразуване преразглежда групи обикновените разтвори тригонометрични уравнения. В третата част се занимава с нестандартни тригонометрични уравнения, които се основават на решения функционалния подход. Четвъртият раздел се занимава с тригонометрични неравенство. Детайли обсъжда методи елементарни тригонометрични разтвори на неравенства, като единица кръг, и така.
;. т.е. ; Общо разтвор. къде. Метод 2: Помислете за друг начин за намирането на решения LDE с две неизвестни, и за това ние считаме, уравнението на формуляра. Уравнения от този тип се наричат линейни хомогенни диофантово уравнение (линейни обикновени диференциални уравнения). Изразяване на неизвестен. чрез да се стигне до непознатото От х трябва да е цяло число, където -. произволно число. Средства.
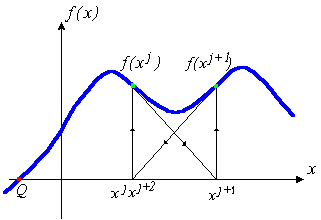
ако началната точка на подход е далеч от точката на решение, на метода на Нютон - Raphson не може да се сближат изобщо. Геометричната тълкуването не е конвергентен Newton - метод Raphson е показано на фиг. 1b. Задача Алгоритъм: намиране на решение на уравнение (1) Вход: първоначалното приближение x0 точност (брой повторения I) Резултат: Xi - разтвор на уравнение (1) Инициализация: изчисли F '(Х0) стъпки.