Дискретните случайни величини
Случайна променлива, наречена стойността на променливата, която е резултат от всеки тест предварително отнема един неизвестен стойност, която зависи от неочаквани събития. Случайни променливи са обозначени с главни латински букви: $ X, \ Y \ Z, \ \ точки $ според вида на случайни величини могат да бъдат дискретни и непрекъснати.
Дискретна случайна променлива - тя е случайна променлива, чиято стойност може да бъде не повече от изброимо, че е било ограничено или изброимо. Под countability което означава, че стойностите на случайна променлива може да се изброят.
Пример 1. Ето някои примери за дискретни случайни величини:
а) броя на посещенията на целта от $ N $ снимки са възможните стойности на $ 0, \ 1, \ \ точки, \ N $.
б) броят на герба на падналия монета жребия, където възможните стойности на $ 0, \ 1, \ \ точки, \ н $.
в) брой на пренощувалите на борда на корабите (изброимо множество стойности).
ж) броя на обажданията, идващи в централата (изброимо множество стойности).
1. Закон дискретни вероятностно разпределение на случайната променлива.
Дискретна случайна променлива $ X $ могат да вземат стойностите $ x_1, \ точки, \ x_n $ с (x_1 \ вдясно), \ \ точки, \ р \ ляв (x_n \ вдясно) $ вероятност $ р \ лявата. Съответствието между тези стойности и техните вероятности се нарича закон на дискретна случайна променлива. Като правило, тази кореспонденция е даден от масата на първия ред на който да показва стойностите $ x_1, \ точки, \ x_n $, а на втория ред, съответстващ на тези стойности на вероятностите $ p_1, \ точки, \ p_n $.
$ \ Започнете
\ hline
x_i x_1 x_2 \ точки x_n \\
\ hline
p_i p_1 p_2 \ точки p_n \\
\ hline
\ Край $
Пример 2. Нека случайна променлива $ X $ - броят на спада точки при жребия на един зар. Такова случайна променлива $ X $ може да следните стойности $ 1 \ 2 \ 3 \ 4 \ 5 \ 6 $. Вероятността за всички тези стойности са равни на $ 1 / $ 6. Тогава законът на разпределение на случайна променлива $ X $:
$ \ Започнете
\ hline
1 2 3 4 5 6 \\
\ hline
1/6 1/6 1/6 1/6 1/6 1/6 \\
\ hline
\ Край $
2. очакването на дискретна случайна променлива.
Очакването на случаен принцип количеството определя неговата "център" стойност. За дискретна случайна променлива очакване се изчислява като сумата на стойностите $ x_1, \ точки, \ x_n $ съответстващи на тези стойности на вероятностите $ p_1, \ точки, \ p_n $, че е: $ M \ наляво (X \ дясно) = \ сума ^ n_ $. В англоезичната литература се използва друга бройна $ E \ ляв (X \ вдясно) $.Свойства на очакването за $ М \ напуснали (X \ вдясно) $:
- $ М \ наляво (X \ вдясно) $ намира между най-малките и най-големите ценности на случайна променлива $ X $.
- Очакване на най-константа е постоянна, т.е. $ М \ наляво (C \ вдясно) = C $.
- Константа, може да бъде взето в знак на математическото очакване: $ М \ ляв (CX \ вдясно) = CM \ наляво (X \ вдясно) $.
- Математическият очакването на сумата от случайни величини е равна на сумата от техните математически очаквания: $ М \ ляв (X + Y \ вдясно) = M \ наляво (X \ вдясно) + M \ наляво (Y \ вдясно) $.
- Математическият очакването на продукта на независими случайни величини е равна на произведението на техните математически очаквания: $ М \ наляво (XY \ вдясно) = M \ наляво (X \ вдясно) М \ ляв (Y \ вдясно) $.
Пример 3. Ние считаме, очакването на случайна променлива $ X $ Пример $ 2 $.
Ние можем да забележим, че $ М \ наляво (X \ вдясно) $ намира между най-ниската ($ 1 $) и най-големият ($ 6 $) стойности на случайна променлива $ X $.
Пример 4. Известно е, че математическото очакване на случайна променлива е равна на $ X $ $ М \ наляво (X \ вдясно) = $ 2. Намери очакването на случайна променлива $ 3X + $ 5.
Използвайки горните свойства, да $ M \ наляво (3X + 5 \ дясно) = М \ наляво (3 х \ дясно) + M \ наляво (5 \ дясно) = 3M \ наляво (X \ дясно) + 5 = 3 \ cdot 2 + 5 = $ 11.
Пример 5. Известно е, че математическото очакване на случайна променлива е равна на $ X $ $ М \ наляво (X \ вдясно) = $ 4. Намери очакването на случайна променлива $ 2 x-9 $.
Използвайки горните свойства, да $ M \ наляво (2Х-9 \ дясно) = М \ наляво (2Х \ дясно) -М \ наляво (9 \ дясно) = 2М \ наляво (X \ дясно) -9 = 2 \ 4 cdot -9 = -1 $.
3. дисперсия на дискретна случайна променлива.
Възможните стойности са случайни величини, равни на средната стойност може да варира пръснати из техните средни стойности. Така например, в две групи студенти, средната оценка за изпита по теория на вероятностите е равно на 4, но в една група са всички horoshist, а в другата група - само troechniki и почести. Затова има нужда от такива числени характеристики на случайни величини, които ще покажат на разпространението на ценностите на случайна променлива за неговото очакване. Тази характеристика е вариацията.
Дисперсията на дискретна случайна променлива $ X $ е:
В англоезичната литература, като се използва нотация $ V \ ляво (X \ вдясно), \ Var \ наляво (X \ вдясно) $. Много често дисперсия $ Г \ отляво (X \ дясно) $ изчислява по формула $ Г \ отляво (X \ дясно) = \ сума ^ N _- ^ 2 $.дисперсионни свойства на $ D \ напуснали (X \ вдясно) $:
- Вариацията е винаги по-голям или равен на нула, т.е. $ D \ наляво (X \ вдясно) \ GE 0 $.
- Дисперсия на константи е нула, т.е. $ D \ наляво (C \ дясно) = 0 $.
- Постоянен фактор може да се приема като знак за дисперсия условие квадратен него, т.е. $ D \ наляво (CX \ вдясно) = C ^ 2D \ наляво (X \ вдясно) $.
- Вариацията на сумата от независими случайни величини е равна на сумата от техните отклонения, т.е. $ Г \ наляво (X + Y \ дясно) = D \ наляво (X \ дясно) + D \ наляво (Y \ дясно) $.
- Отклонението от разликата на независими случайни величини е равна на сумата от техните отклонения, т.е. $ Г \ наляво (X-Y \ дясно) = D \ наляво (X \ дясно) + D \ наляво (Y \ дясно) $.
Пример 6. Ние изчисляване на разсейването на случайна променлива $ X $ $ от Пример 2 $.
Пример 7. Известно е, че вариацията на случайна променлива е равна на $ X $ $ D \ наляво (X \ вдясно) = $ 2. Намерете отклонението на случайната променлива $ 4X + 1 $.
Използвайки горните свойства, намери $ Г \ лявата (4Х + 1 \ дясно) = D \ наляво (4Х \ дясно) + D \ наляво (1 \ дясно) = 4 ^ 2D \ наляво (X \ полето) + 0 = 16D \ наляво (X \ вдясно) = 16 \ cdot 2 = $ 32.
Пример 8. Известно е, че вариацията на случайна променлива е равна на $ X $ $ Г \ наляво (X \ дясно) = 3 $. Намерете отклонението на случайната променлива $ 3-2X $.
Използвайки горните свойства, намери $ Г \ наляво (3-2X \ дясно) = D \ наляво (3 \ дясно) + D \ наляво (2Х \ дясно) = 0 + 2 ^ 2D \ наляво (X \ дясно) = 4D \ наляво (X \ вдясно) = 4 \ cdot 3 = $ 12.
4. Функцията на дискретна случайна променлива разпределение.
Метод представителство на дискретна случайна променлива разпределение като серия не е единственият и най-важното не е универсален, тъй като непрекъснато случайна стойност не може да се настрои с помощта на разпределение на брой. Има и друг начин за представяне на случайна променлива - функция дистрибуция.
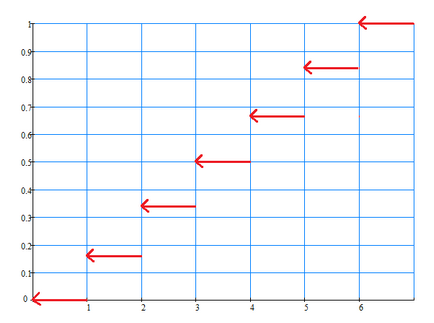
Разпределение функция на случайна променлива $ X $ е функция $ F \ ляв (х \ вдясно) $, който определя вероятността случайна променлива $ X $ отнема стойност по-малко от фиксирана стойност от $ х $, т.е. $ F \ наляво (х \ вдясно) = P \ наляво (X Свойствата на функцията на разпределение: Пример 9. Нека да се намери функция на разпределение F $ \ ляво на (х \ вдясно) $ за закона на разпределение на дискретни случайни променливи $ X $ Пример $ 2 $. $ \ Започнете Ако $ х \ ле 1 $, след това, очевидно, $ F \ оставени (х \ полето) = 0 $ (включително $ х = 1 $ $ F \ наляво (1 \ дясно) = \ наляво P (X <1\right)=0$). Ако $ 1 Ако $ 2 Ако $ 3 Ако $ 4 Ако $ 5 Ако $ х> 6 $, след $ F \ наляво (х \ дясно) = P \ наляво (X = 1 \ дясно) + P \ наляво (X = 2 \ дясно) + P \ наляво (X = 3 \ дясно) + P \ наляво (X = 4 \ дясно) + P \ наляво (X = 5 \ дясно) + P \ наляво (X = 6 \ полето) = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1 $. разпределение График функция $ F \ ляв (х \ вдясно) $:
\ hline
1 2 3 4 5 6 \\
\ hline
1/6 1/6 1/6 1/6 1/6 1/6 \\
\ hline
\ Край $