Дискретните случайни величини, по-високи математика
Дискретна случайна променлива.
1. Определяне на случайна променлива, дискретна случайна променлива. Право и полигон DSV разпределение.
I. Определяне на случайна променлива, дискретна случайна променлива. Право и полигон DSV разпределение.
Когато хвърляне на зарове може да се появи числата 1, 2, 3, 4, 5 и 6 предварително да се определят възможните резултати е невъзможно, тъй като зависи от много случайни фактори, които не могат да бъдат напълно отчетени. В този пример се утаява брой точки е произволна стойност, и числата 1, 2, 3, 4, 5 и 6, има възможни стойности на това количество.
Случайна стойност - стойността на който получава определена числова стойност в резултат на опит с произволни резултати и предварително известни, които един. Случайна стойност (накратко: N) означаваме главни букви и стойностите, взети от тях - малки букви
От горните примери се вижда, че случайната променлива X може да приеме една от следните възможни стойности: 1, 2, 3, 4, 5, 6. Тези стойности са разделени една от друга чрез празнини, в които не потенциал H. стойност По този начин, този пример се приема, SV отделни изолирани възможни стойности.
Дискретни (прекъснат) се нарича случайна променлива, която се отделни изолирани възможни стойности с някои вероятности. Броят на възможните дискретни стойности на случайна променлива може да бъде ограничен или безкраен.
дискретна случайна променлива закон разпределение се нарича кореспонденцията между възможните стойности и техните вероятности; тя може да уточни табличен аналитично (във формулата) и графично.
Разпределението на X DSV е удобно, за да определите следната таблица
наречен следващата дистрибуция. Тук е възможно стойности NE X в горния ред на таблицата са разположени в определен ред, и в долната част - съответните вероятности.
Графично разпределение брой е изобразена като многоъгълник (или многоъгълник а) разпределение.
1.1. В чекмеджето 2 и 4 нестандартни стандартни части. От него отстраняват последователно елементи в първи епизод на стандарт парче. Изграждане на броя на разпределение полигон DSV - броят на извлечените компоненти.
Помислете за всички възможни стойности, които могат да предприемат случайни променливи (CO):
- първият извади стандартна част;
- Първият елемент извадени нестандартно, вторият стандарт;
- Първата част нестандартен, нестандартно втората част трета стандарта за компонент.
Съответните вероятности намирате с вероятност умножение правило (имайте предвид, че събитията зависим):
Тогава законът на разпределение на дискретна случайна променлива X е под формата:
Ние изграждане на многоъгълник разпределение, поставяне на оста на абсцисата (ОХ) DSV стойност X, и Ординатната ос (OY), съответстващ вероятности:
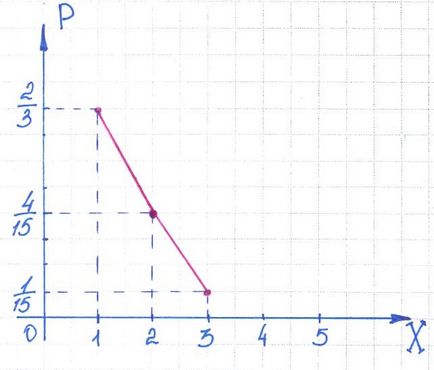
1.2. В играта, съдържащ 20 членове, има четири продукти с дефекти. Произволно избрани три продукта, за да се провери тяхното качество. Construct разпределение брой на броя на дефектни продукти, съдържащи се в пробата.
- броят на дефектните продукти, съдържащи се в пробата.
Помислете за всички възможни стойности, които могат да предприемат случайни променливи (CO):
- не се вземат проби на продукта не е дефектен, т.е. Всички продукти отговарят на стандарта;
- проба съдържа един продукт с дефект и две стандартни продукти;
- проба съдържа два продукта с дефекта и един стандартен продукт;
- проба съдържа три продукти с дефект;
Ние намираме съответните вероятности:
Тогава законът на разпределение на дискретна случайна променлива X е под формата:
1.3. Три показалка, което води огън по предназначение, направих един изстрел. Вероятност от удари цел са съответно 0.5, 0.6, 0.8. Изграждане на брой и разпределение на полигон SW X - броя на посещенията в целта.
Нека вероятността за 1-ви, 2-ри и 3-ти стрелците са, съответно, тогава вероятността за инциденти са равни. От предишни изследвания, ние трябва да помним, как да се отнасят противоположни събития :.
Помислете за всички стойности, които могат да DSV X - броя на посещенията в целта.
- нито един от стрелците не да достигне целта;
- един от стрелците постигне целта;
- две стрелци да достигне целта;
- три стрелка целта.
Ние намираме съответните вероятности:
тип запис означава, че първия стрелка хит, а другите две пропуснати, подобни съображения се прилагат за другите условия.
(Двама от тримата постигне целта);
(Три стрела удари целта)
Намираме вероятностите на всички М DSV стойности по-малки или равни на 2
Литература: