Дискретна случайна променлива - studopediya

Специално място сред случайни дискретни променливи да вземе стойности от биномиално закон за разпределение:

- на броя на повторения на едно събитие в независимите повтарят изпитанията,

- честотата на поява на събитие в независимите повтарят изпитанията.

Характеристики на дискретна случайна променлива:

- стандартно отклонение.

При изчисляване на дисперсия собственост се използва: D (X) = М (х 2) -М 2 (X).

За биноминално разпределени случайни величини могат да се прилагат за изчисляване на формули известни характеристики:

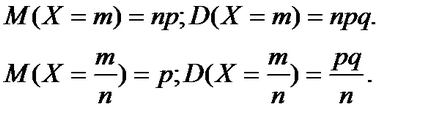
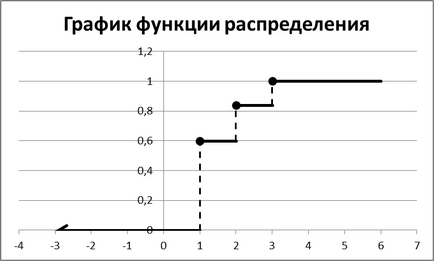
функцията на разпределение на дискретна случайна променлива:

функцията на разпределение на дискретна случайна променлива е по части константа, има прекъсвания в точките с координати равни на стойностите на случайна променлива.

Пример 3.1. Капитанът "N" Има три акционер на различни компании. Вероятността за получаване на доходи по пакет от акции е равна на 0,6. Бъдете закон случайна променлива X - брой на печелившите пакети от акции от майстор да се определи нейната средна и отклонения. Намерете вероятността, че този господин не е по-малко от две печеливши дялове.

Решение. За да се осъществи по един избран пакет акции на събитията: той няма да донесе доход - или ще - А. Според проблемът с вероятности Р (A) = 0.6, P =; Р () = 0,4 = р. Вероятностите за събития са постоянни за всички пакети от акции, следователно, да се появят независими многократните опити, от които малко п = 3.

X - случайна променлива, а именно броят на печелившите пакети от акции от г-н Разглеждане на събитие Xm = М, състоящ се в това, че в случай, че се появява в п независими проучвания м пъти. За да се определи вероятността за това събитие трябва да се прилага на Бернули формула. Случайна променлива има биномно разпределение:

Пример 3.3. Топките 10 урна: 4 бели, а останалата част - черен. Намерете правото на случайна променлива разпределение на X - броят на бели топки, освен ако не го един по един, без да погледне отстранен 3 топки. Намери очакването и отклонението на случайната променлива X. Намерете вероятността, че броят на бели топки извадени е повече от очакванията.

Решение. X - брой на бели топки 3 комбинират. Разпределението на работа и изчисления относно характеристиките на случайна променлива:

Характеристики на случайна променлива X - брой на бели топки 3 взети:

Дисперсия - D (X) = М (х 2) -М 2 (X) = 2- (1,2) 2 = 0,56.

Вероятността, че броят на бели топки ще бъдат извадени над очакванията:

Разпределението на дискретна случайна променлива X в тази задача се нарича хипергеометричното закона за разпределение.