тригонометрични формули

Взаимна от основните тригонометричните функции, които косинус както и задължително, допирателна и котангенс - наричат ​​тригонометрични формули. Поради факта, че много голям брой от взаимоотношения, съответно, и формулата е не по-малко. Част формули съчетава тригонометрични функции в зависимост от ъгъла, който може да бъде или множествена или еднакви. Тя може да се изрази по тангенс на ъгъла на половината. Само чрез намаляване на степента.






Ние ще анализираме най-основните тригонометрични формули. С помощта на които можете да решите повечето от тригонометрични задачи. За допълнително удобство, да ги комбинирате по стойност, в съответствие с таблиците.

Нека започнем с тригонометрични идентичност.

Бази в тригонометрични идентичности, определени отношения задължително и косинус, тангенс и котангенс в единия ъгъл. И от тяхното определяне и единица кръга. Осигуряване на възможност да се изтъкне, чрез всяка друга функция.

На следващо място, разгледа тригонометрични формули задействане.

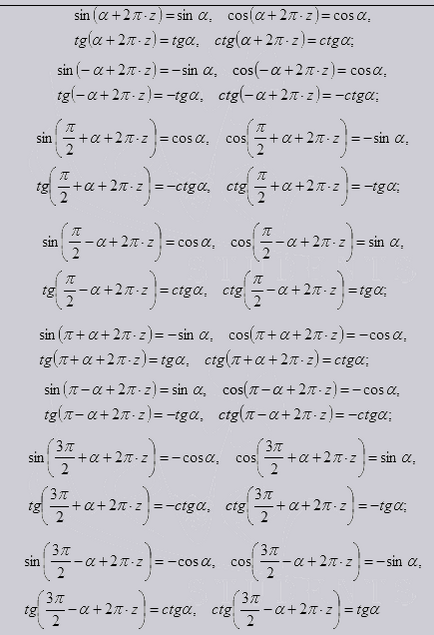
Те произтичат от свойствата на Синиш, уют и тангенти cotangents. По този начин, експресиращи свойства такива функции като: честота, симетрия и изместване надясно под внимание. също така предоставя възможност за работа с ъгли от порядъка на до 90 градуса и произволни ъгли.

Формула за добавяне.







От тези формули е очевидно, че функциите на сумата или разликата на две ъгли са получени от тях като тригонометрични функции. Също така е в основата на формулите на двоична, троична и други ъгли.

Формулата за двоичен, трикомпонентни и други ъгли.

Те показват, че тригонометрични функцията на двойни, тройни или всеки ъгъл каквато получен от TF единични ъгли.

Както и единични, двойни, тройни и т.н. има и ъгли половина

От формулите за половин ъгъл виждаме, че той излиза от косинус на ъгъла на цялото.

Както има степени на методи за намаляване изглеждат:

С използването им може да се понижи функцията на първа степен. Взаимодействаме с естествената сила на функцията за превод само Синиш и уют на множество ъгли в първа степен.

Сумата и разликата от тригонометрични функции.

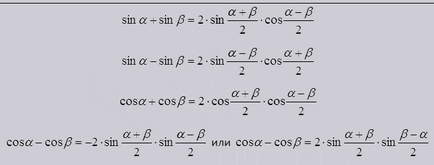
Да опрости тригонометрични изразяване, и да фактор Синиш и уют.

Продуктът на синус, косинус, и една за друга.


Методът на универсалната тригонометрични смяна.

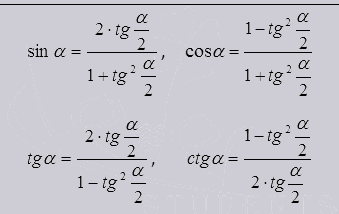
Такова заместване е удобно, защото функции са получени без корени.