лекция №6

Интерполация, Лагранж интерполация полиноми и Нютон.

Общи проблеми на интерполация. Параболична интерполация.

При решаването на много проблеми при използването на определени функции на маса. Например, ако установим емпирично поредица от стойности на функцията за изчисляване на стойностите, които не са включени в таблицата, е възможно да се избере друга, по-проста функция, по начин, затворете това.

Има различни начини за получаване на тези функции. Един от тях - интерполация.

Като цяло, проблемът на интерполация е формулиран, както следва:

Нека N + 1 в точките

дадени стойности на функцията

Задължително да вземете сравнително проста funktsiyuφ (х), което отговаря на следните условия:

б) за останалите стойности на х в областта на приблизителното уравнение трябва да се увери

Функцията φ (х) nazyvaetsyainterpoliruyuschey,

процеса на неговото изграждане - чрез интерполация,

и x0, x1, x2, ..., хп. в която стойностите на интерполиране функция трябва да съвпадат с предварително определени стойности на функция интерполиране -uzlami.

Точка х. където изчислената стойност на функция е (х) чрез funktsiiφ (х). nazyvaetsyatochkoy интерполация.

Параболична интерполация. Интерполиране функция обикновено се избира от определен клас функции. Често, като такава функция е взето mnogochlenFn (х), който nazyvaetsyainterpolyatsionnym полином.

Интерполация използвайки полином наречен параболичен интерполация, геометричен смисъл от които е, че графиката на F функция (х) се заменя със парабола-графика mnogochlenaFn (х); докато графики imeyutn + 1 обща точка.

Следователно, проблемът на параболичен интерполация е формулиран, както следва:

Нека стойностите на F функция (X) са определени на п + 1 интерполация възел

Като интерполиращите полином функции избират

и изискват възлите на ценности интерполация полином интерполация съвпадат с ценностите на тази функция:

За да изчислим неизвестните коефициентите на полинома, въз основа на състоянието (4) образуват система от уравнения:

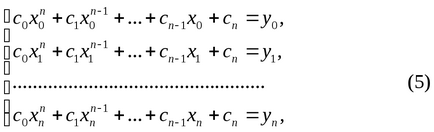
Форма детерминантата на системата (5):

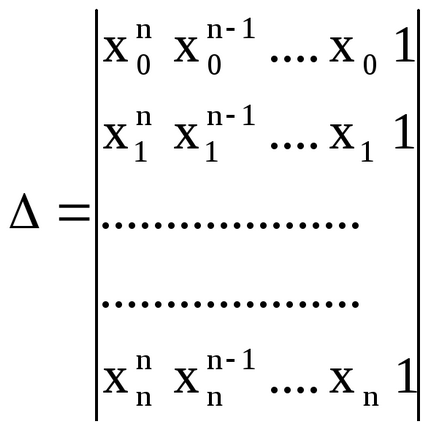
Този фактор е известно от курса на висшето алгебра като определящ фактор Vandermonde.

Тъй като интерполация възли x0, Х1, Х2, ..., хп са различни, тогава   0, следователно, линейната система (5) има уникален разтвор, което означава, наличието и уникалността на интерполация полином на Fn (х).

Трябва да се отбележи, че различните записи на полином интерполация, използвани при решаване на различни проблеми.

Lagrange интерполация полином

Според условията (1), (2), е показано на φ (х) функционира. mnogochlenn напише втора степен.

В същото време, другите условия на полином (6) трябва да бъде нула, т.е.

По този начин, ние формулирани изискванията за пи фактор (х). а именно:

Фактор пи (х) полином nazyvayutvspomogatelnym stepenin.

Като се има предвид имота (8) и изискването, че полином пи (х) е stepenn. Пишем:

където коефициентът CI.

За да се определи CI завой на изискването (7). От това следва:

Чрез заместване (10) в (9) води до получаване на крайния израз за пи (х):

Вграден полином (11), например, в точка x0 на znacheniep0 получава (x0) = 1, и в други възли - стойности равна на нула.

Полином Р1 (X) в tochkex1 ще бъде една и останалите възли е равно на 0, и т.н.

По този начин, спомагателни полином PI (х) напълно отговаря на изискванията (7), (8), а втората степен mnogochlenn-

Това е интерполация полином на Лагранж.

Забележка: Lagrange полином подходящо да се използва в задачата за възстановяване на функция е (х). когато точката е по-близо interpolyatsiix ktsentru решетка.

Ние считаме, е функция (х). Задава таблица:

Следователно, построена полином отговаря на състоянието на главния (1).

По този начин, тестове алгоритъм са както следва:

разположени един след друг като XI на ценности точки маса и интерполация за да се получи съответната стойност funktsiifi (при условие трябва да бъде изпълнено за правилно работеща програма (1)).

зададен като стойностите на интерполация от множество пиксели, които не са възли на мрежата, както и проверка на състоянието (2).

оценка за грешка Lagrange интерполация формула

елемент разлика Rn (х) nazyvaetsyaostatochnym формула Лагранж. ZnachenieRn (х) е равна на грешката, която се получава чрез заместване на стойностите на функцията F (х) стойност интерполация mnogochlenaFn (х).

е възможно да се получи формула за срока на остатък

С формула (13) могат да бъдат написани по различен начин:

тогава ние получи оценка на остатъка:

Пример. За funktsiiu = 2Х конструиране на интерполация полином Lagrange чрез интерполиране точка възли

Изчисляваме съответните стойности на функцията:

формула на Лагранж намираме:

Ние оценка на грешката, която се получава чрез заместване на функция Y = 2x mnogochlenomF3 (х). производно четвърти порядък

В интервала [1; 2] funktsiya2x се увеличава, така че 0<2x <= 4.

С формула (15) получаваме:

На разглежданите Lagrange полином обикновено се използва в проблеми на възстановяване на функция е (х). когато точката на вмъкване се намира по-близо до центъра на решетката.

Ако точка х интерполация се намира по-близо до краищата на мрежата, по-добре е да се използва полином на Нютон. Има две възможности:

интерполация точка х е vblizipervogo setkih0 възел (NyutonaI полином);

интерполация точка х е vbliziposlednego setkihn възел (NyutonaII полином).

Забележка. Строителство на Лагранж полином на базата на суб mnogochlenepi (х).

В основата на изграждането е концепцията за полином на ограничен разликата Нютон.

Ние се определи понятието крайна разлика.

Нека масата за функция е зададена с постоянен shagomh: